Fit an inscribing circle to a shape in OpenCV

The largest possible circle that can be drawn interior to a plane figure is called an inscribing circle. This can easily be fitted to a binary shape in OpenCV.

Let’s use a 939×1100 px RGB image of Australia, supplied by the Bureau of Meteorology, for this example.

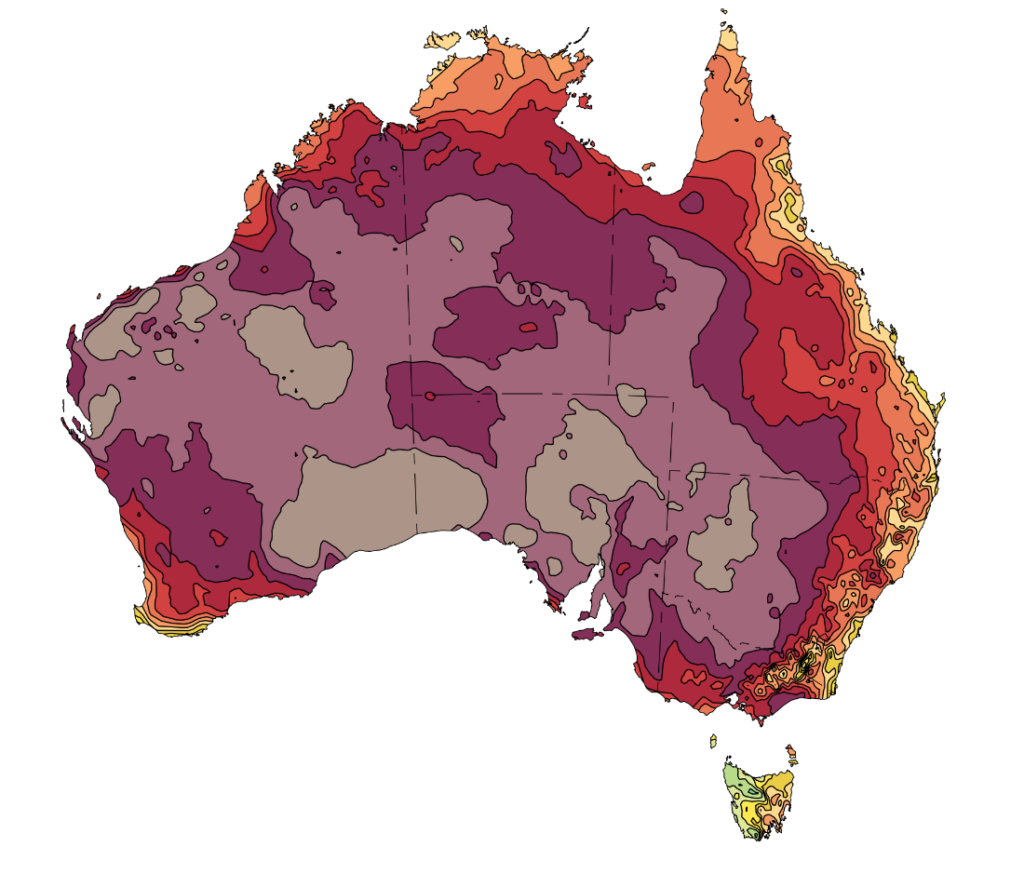
To begin, libraries need to be loaded and the image needs to be read into OpenCV. I am using OpenCV 4.5.3.56 with Python (3.9.7) on Windows 11. The other required libraries are Matplotlib (I am using 3.4.3) and NumPy (I am using 1.21.2):

import cv2
import matplotlib.pyplot as plt
import numpy as np

img = cv2.imread("/path/to/australia.png")

Once the image is read-in, it needs to be converted from RGB to 8-bit greyscale (uint8):

grey = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)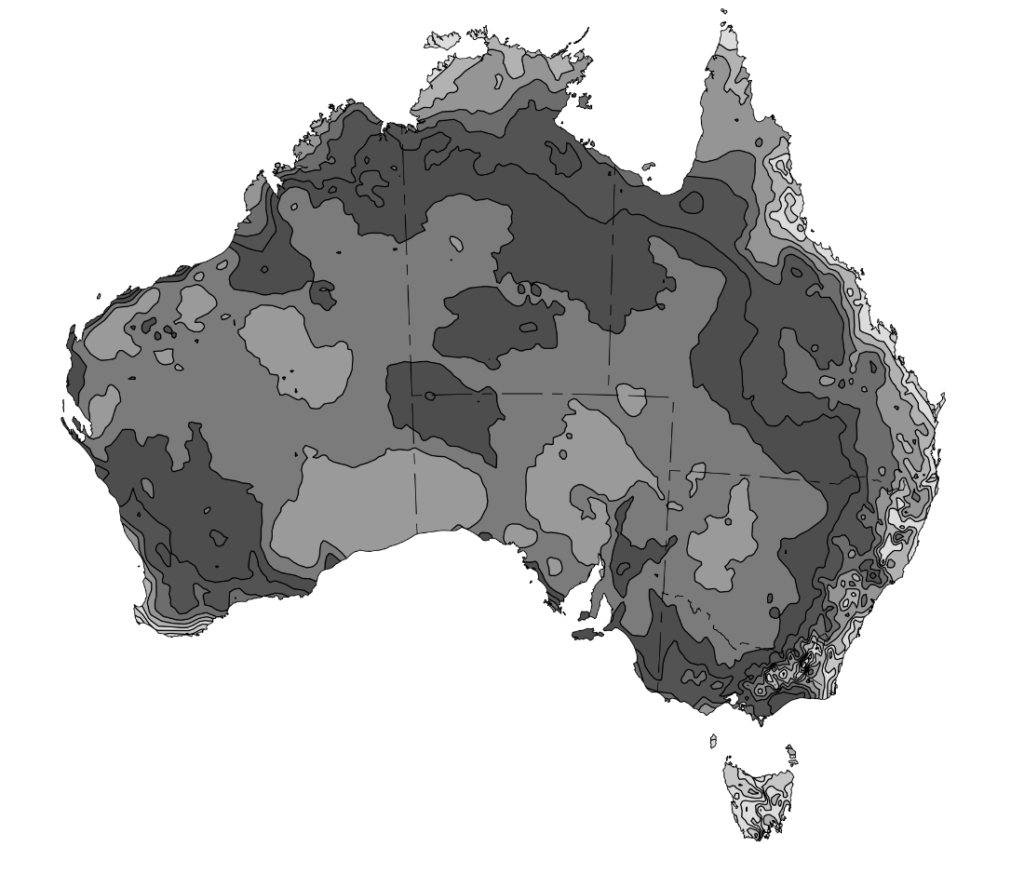

Next, the image needs to be thresholded into a binary such that the foreground (Australia) is white:

ret, thresh = cv2.threshold(grey, 254, 255, cv2.THRESH_BINARY)
thresh_inv = cv2.bitwise_not(thresh)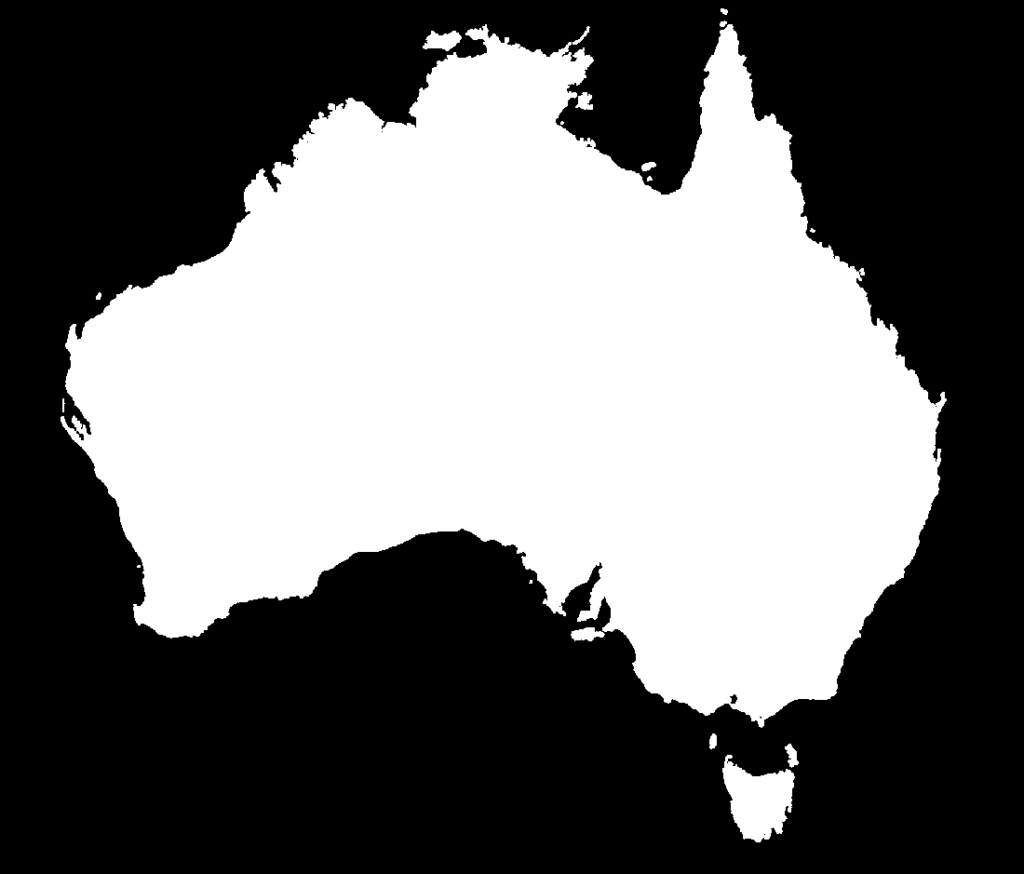

Next, perform a distance transform on the binary image:

distance = cv2.distanceTransform(thresh_inv, cv2.DIST_L2, cv2.DIST_MASK_PRECISE)

For the inscribing circle, the greatest value in the distance transform is the radius and its position is the centre. These values can be extracted from the distance transform using the cv2.minMaxLoc() function and then applied to the cv2.circle function to draw the circle on the original image.

_, max_val, _, centre = cv2.minMaxLoc(distance)
circle = cv2.circle(img, centre, int(max_val), (255, 0, 0), 2)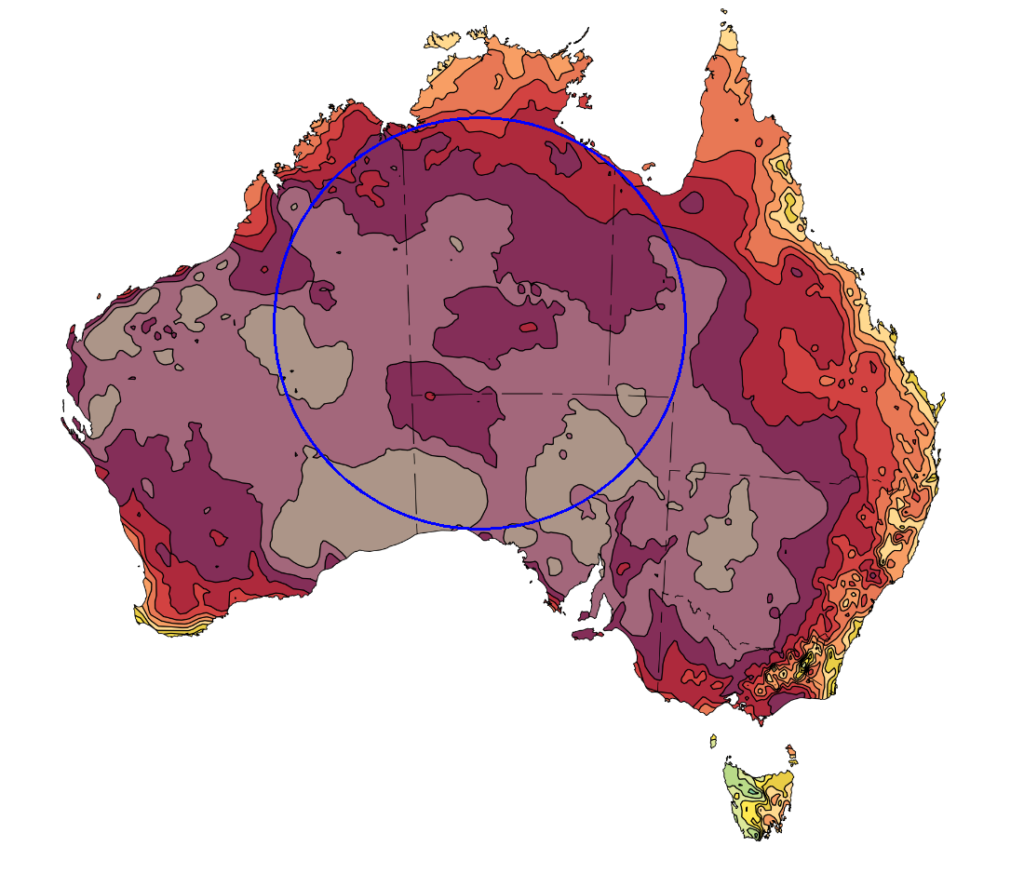

These values can also be reported:

print("Max value:", max_val, "Position:", centre)

Max value: 221.73182678222656 Position: (515, 347)

Have Your Say

Δ